What I want to do in this section is calculate the radius of exoplanet GJ4276.
What I have done to calculate what I want has been to look for the coordinates of cepheus (but not all of cepheus, a majority) which are:
- Right ascension: between 20h 50m and 23h 10m.
- Declination: between 58ºand 88º.
https://www.iau.org/public/images/detail/cep/
Later I have gone from hours to degrees to find the coordinates in the list of exoplanets where it indicates the declination and right ascension in degrees and there I look for an exoplanet that is within the obtained coordinates. An exoplanet that is within these coordinates is GJ4276.
Then I have looked for this exoplanet in the exoplanets of NASA and I have looked on this page for the exoplanet GJ4276 where I put a website where the light curve is.
https://exoplanetarchive.ipac.caltech.edu
In this article I have found the variation of light that is 0.02 in so much for one that corresponds to 2%. With this data I have calculated the distance of the exoplanet.
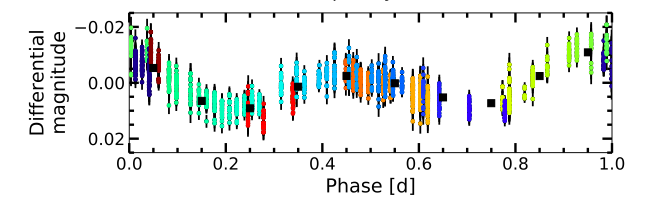
https://www.aanda.org/articles/aa/pdf/2019/02/aa34569-18.pdf
This figure shows us, made by Naggel et al. 2019, that this exoplanet varies by 2%. With this 2% and the radius of the star I have already been able to calculate the radius of the planet. This calculation nobody has done before, because the article where I found the radius of the star didn't put the radius of the planet because most likely nobody has seen this article because it is very recent (2019).
http://exoplanet.eu/catalog/gj_4276_b/
The results I have obtained are the following:
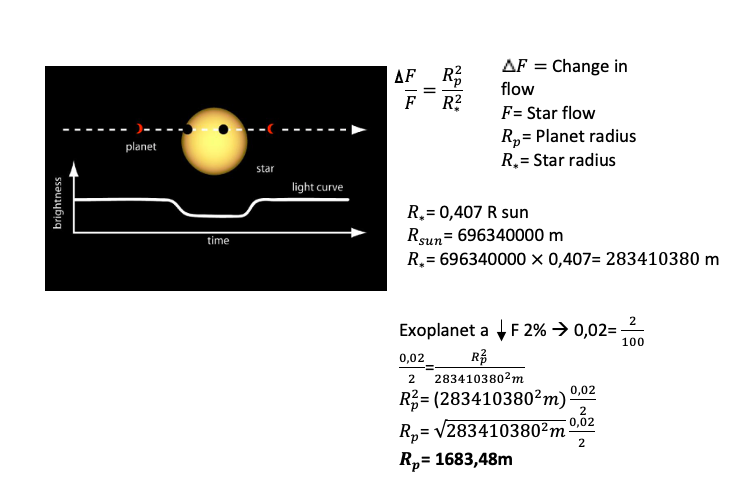
The radius of planet is 1683,48 m.